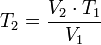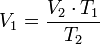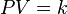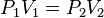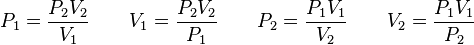La ley de Gay-Lussac establece que la presión de un volumen fijo de un gas, es directamente proporcional a su temperatura.
- Si el volumen de una cierta cantidad de gas a presión moderada se mantiene constante, el cociente entre presión y temperatura (kelvin) permanece constante:
o también:
donde:
- P es la presión
- T es la temperatura absoluta (es decir, medida en kelvin)
- k3 una constante de proporcionalidad
- Supongamos que tenemos un gas que se encuentra a una presión
 y a una temperatura
y a una temperatura  al comienzo del experimento. Si variamos la temperatura hasta un nuevo valor
al comienzo del experimento. Si variamos la temperatura hasta un nuevo valor  , entonces la presión cambiará a
, entonces la presión cambiará a  , y se cumplirá:(left)donde:
, y se cumplirá:(left)donde: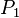 = Presión inicial
= Presión inicial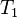 = Temperatura inicial
= Temperatura inicial = Presión final
= Presión final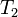 = Temperatura final
= Temperatura final- Experimento de la Ley Gay- Lussac
- Ejercicios Propuestos
- 1.- Un gas, a una temperatura de 35°C y una presión de 440 mm de Hg, se calienta hasta que su presión sea de 760 mm de Hg. Si el volumen permanece constante, ¿Cuál es la temperatura final del gas en °C?
- 2.- La presión del aire en un matraz cerrado es de 460 mm de Hg a 45°C. ¿Cuál es la presión del gas si se calienta hasta 125°C y el volumen permanece constante.




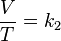
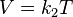
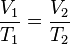
 = Volumen inicial
= Volumen inicial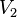 = Volumen final
= Volumen final